標題：CTF之crpto練習三

[taibeihacker]

DES弱加密之easy_BlockCipher​

下載附件得到2個文件：https://adworld.xctf.org.cn/media/task/attachments/5b8bcb28546b4423b481b13149abc99f.zip

分析題目，題目中給出了加密時的代碼。
des-ofb.py:
from Crypto.Cipher import DES
f=open('key.txt', 'r')
key_hex=f.readline()[:-1] # discard newline
f.close()
KEY=key_hex.decode('hex')
IV='13245678'
a=DES.new(KEY, DES.MODE_OFB, IV)
f=open('plaintext', 'r')
plaintext=f.read()
f.close()
ciphertext=a.encrypt(plaintext)
f=open('ciphertext', 'w')
f.write(ciphertext)
f.close()可知加密時採用了DES算法，並且在OFB模式下對明文進行加密。
因此在已知IV=‘12345678’ 的情況下，只需要知道Key，即可對密文進行破解。
根據已知信息，僅有IV以及未知的Key，所以想到DES加密種存在弱密鑰。在DES 的計算中，56bit 的密鑰最終會被處理為16 個輪密鑰，每一個輪密鑰用於16 輪計算中的一輪，DES 弱密鑰會使這16 個輪密鑰完全一致，所以稱為弱密鑰。
其中四個弱密鑰為：
0x0000000000000000
0xFFFFFFFFFFFFFFFF
0xE1E1E1E1F0F0F0F0
0x1E1E1E1E0F0F0F0F利用四組若密鑰嘗試對密文進行破解。
from Crypto.Cipher import DES
f=open('ciphertext', 'r')
ciphertext=f.read()
f.close()
IV='13245678'
KEY=b'\x00\x00\x00\x00\x00\x00\x00\x00'
a=DES.new(KEY, DES.MODE_OFB, IV)
plaintext=a.decrypt(ciphertext)
print plaintext
KEY=b'\x1E\x1E\x1E\x1E\x0F\x0F\x0F\x0F'
a=DES.new(KEY, DES.MODE_OFB, IV)
plaintext=a.decrypt(ciphertext)
print plaintext
KEY='\xE1\xE1\xE1\xE1\xF0\xF0\xF0\xF0'
a=DES.new(KEY, DES.MODE_OFB, IV)
plaintext=a.decrypt(ciphertext)
print plaintext
KEY='\xFF\xFF\xFF\xFF\xFF\xFF\xFF\xFF'
a=DES.new(KEY, DES.MODE_OFB, IV)
plaintext=a.decrypt(ciphertext)
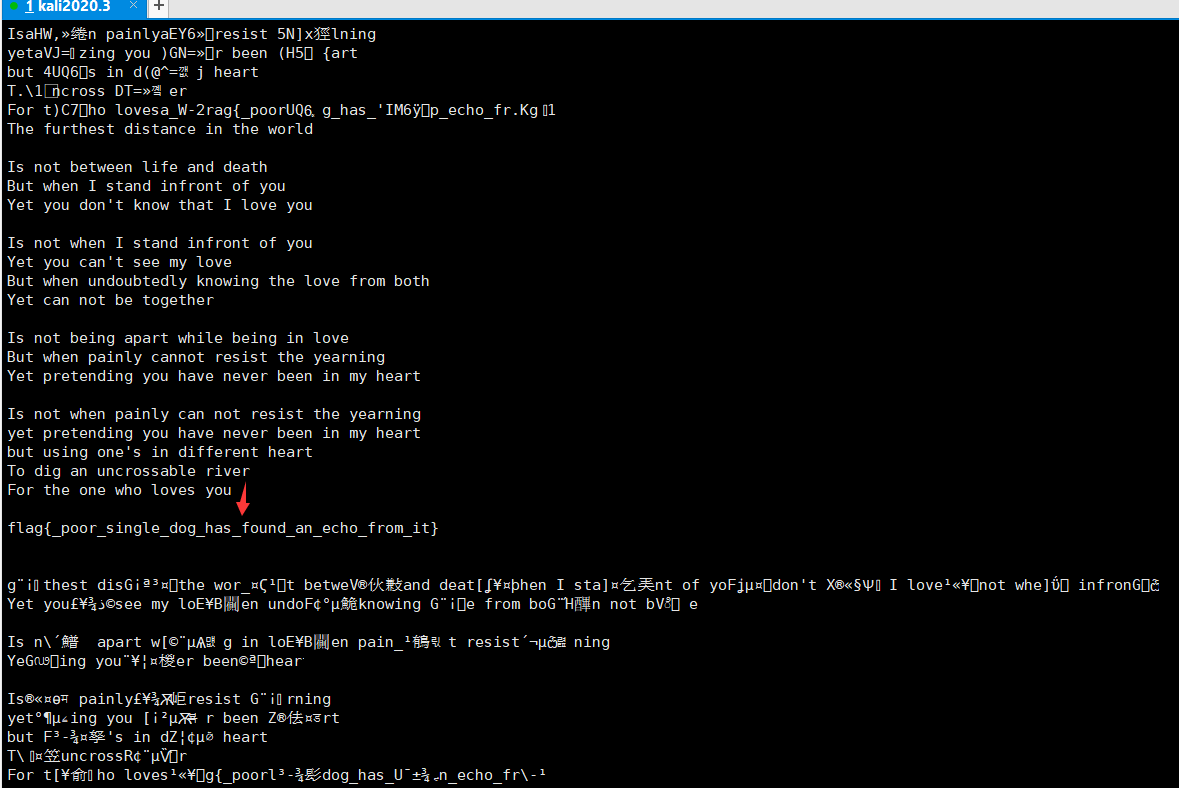
print plaintext從得到的結果中得到明文為莎士比亞的一首詩。

或者腳本：#coding:utf-8
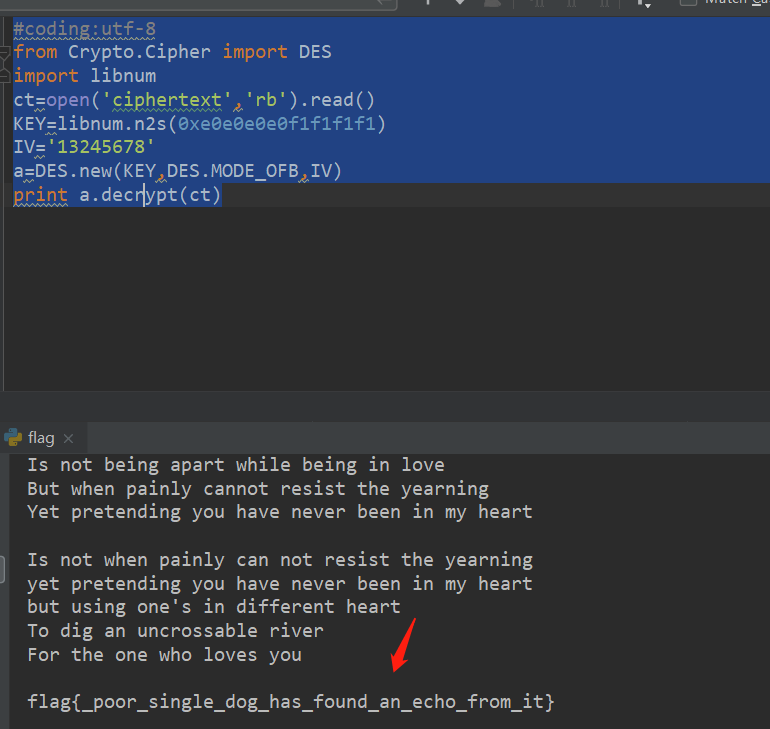
from Crypto.Cipher import DES
import libnum
ct=open('ciphertext','rb').read()
KEY=libnum.n2s(0xe0e0e0e0f1f1f1f1)
IV='13245678'
a=DES.new(KEY,DES.MODE_OFB,IV)
print a.decrypt(ct)

最終得到flag:flag{_poor_single_dog_has_found_an_echo_from_it}

RSA算法之special-rsa​

題目描述：在學習RSA算法時，我發現了一種和RSA具有同等安全性的算法。 對msg.txt加密得到了msg.enc。 $ python special_rsa.py enc msg.txt msg.enc 你能從flag.enc中恢復flag.txt麼？下載附件，裡麵包含了4個文件，如下： https://adworld.xctf.org.cn/media/task/attachments/7a407f44a073442c91fd395b20594f01.zipflag.enc
special_rsa.py
msg.enc
msg.txt
題目的思路是用隱藏的key解密flag.enc文件，閱讀special_rsa.py文件加密和解密過程後，我做了簡單的公式來找到隱藏的key。

偽代碼如下：
flag.sage:
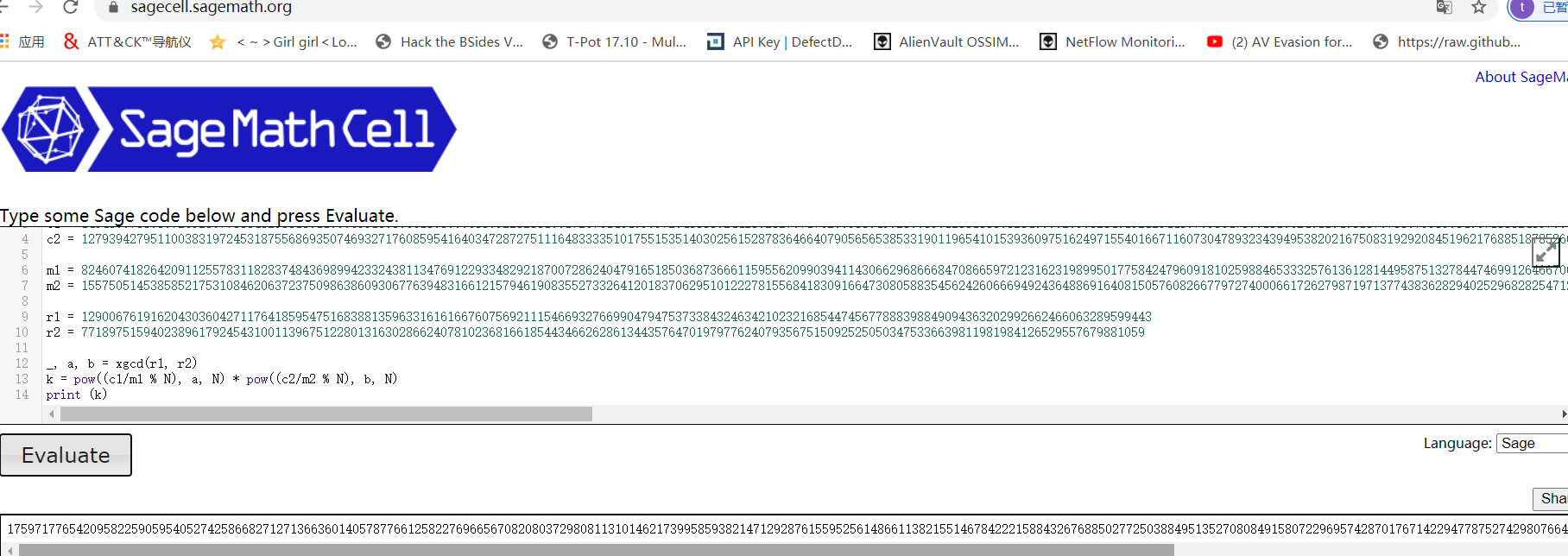
N=2392741101402069577293491676495366164131014848097705664525509819249174035652524067590628570051635757892994011455370097616796996436414961522656868922422802 84616866172935341157887799555978779650445704934575674208747413571865964257536674552668704021545524398996644464136327167476448548975519407775125220449071328 6490564421265538722330241089687108075176822409176093420991798421358551351059761970879768870587680546488010579782938032655939972304809217549220389446875271 8008631464599810632513162129223356467602508095356584405555329096159917957389834381018137378015593755767450675441331998683799788355179363368220408879117131L
c1=1454899738089726523977888482538130110996551898966180809068895223238109172676146495957294338302442802827071762995389459289085912881883932849900295082849152 1254480795364789013196240119403187073307558598496713832435709741997056117831860370227155633169019665564392649528306986826960829410120348913586592199732730 9332598804692297241498873800056273217528434895649843587080133005246405454377037714241681082130455675685950934213662248186095013187836804977633536181101840 78118456368631056649526433730408976988014678391205055298782061128568056163894010397245301425676232126267874656710256838457728944370612289985071385621160886
c2=1279394279511003831972453187556869350746932717608595416403472872751116483333510175515351403025615287836466407905656538533190119654101539360975162497155401 6671160730478932343949538202167508319292084519621768851878526657022981883304260886841513342396524869530063372782511380879783246034751883691295368172069170 9679755613642775140633206919309002580172938717542522097273017192076923217982292767321985217116020802449502958895754233833080997862981844776683028429522156 65734671829249323604032320696267130330613134368640401070775927197554082071807605399448960911234829590548855031180158567578928333030631307816223152118126597
m1=8246074182642091125578311828374843698994233243811347691229334829218700728624047916518503687366611595562099039411430662968666847086659721231623198995017758 4247960918102598846533325761361281449587513278447469912646670073595181813635229344306766552368804895500938525248013046123223735422962819621967953044997110 0680121178300585729736293033897887245193486043559754564221921355168597320820987362390962927832118148501096446065229869005874709029831236523067172379085099 8541956664376820820570709272500330966205578898690396706695024001970727864091436518202414166919020415892764617055978488996164642229582717493375419993187360
m2=1557505145385852175310846206372375098638609306776394831661215794619083552733264120183706295101222781556841830916647308058835456242606669492436488691640815057608266779727400066172627987197137743836282940252968282547129986181482946 3510659258586020732228351258291527965822977048954720558973840956731377322516168809373640494227129998871167089589689796024458501705704779109152762373660542684880052489213039920383757930855300338529058000330103359636123251274293258
r1=12900676191620430360427117641859547516838813596331616166760756921115466932766990479475373384324634210232168544745677888398849094363202992662466063289599443
r2=7718975159402389617924543100113967512280131630286624078102368166185443466262861344357647019797762407935675150925250503475336639811981984126529557679881059
_, a, b=xgcd(r1, r2)
k=pow((c1/m1 % N), a, N) * pow((c2/m2 % N), b, N)
print (k)

得到key：
1759717765420958225905954052742586682712713663601405787766125822769665670820803729808113101462173995859382147129287615595256148661138215514678422215884326 76885027725038849513527080849158072296957428701767142294778752742980766436072183367444762212399986777124093501619273513421803177347181063254421492621011961
得到key，解密flag.enc，得到答案：
port msgpackdef egcd(a, b): if a==0: return (b, 0, 1) else: g, y, x=egcd(b % a, a) return (g, x - (b //a) * y, y)def modinv(a, m): g, x, y=egcd(a, m) assert g==1 return x % mdef pad_even(x): return ('', '0')[len(x)%2] + xdef decrypt(c, k): out='' for r_s, c_s in msgpack.unpackb(c): r=int(r_s.encode('hex'), 16) c=int(c_s.encode('hex'), 16) k_inv=modinv(k, N) out +=pad_even(format(pow(k_inv, r, N) * c % N, 'x')).decode('hex') return outN=2392741101402069577293491676495366164131014848097705664525509819249174035652524067590628570051635757892994011455370097616796996436414961522656868922422802 84616866172935341157887799555978779650445704934575674208747413571865964257536674552668704021545524398996644464136327167476448548975519407775125220449071328 6490564421265538722330241089687108075176822409176093420991798421358551351059761970879768870587680546488010579782938032655939972304809217549220389446875271 8008631464599810632513162129223356467602508095356584405555329096159917957389834381018137378015593755767450675441331998683799788355179363368220408879117131k=1759717765420958225905954052742586682712713663601405787766125822769665670820803729808113101462173995859382147129287615595256148661138215514678422215884326768 85027725038849513527080849158072296957428701767142294778752742980766436072183367444762212399986777124093501619273513421803177347181063254421492621011961print decrypt(open('flag.enc').read(), k)
最終得到flag:
Flag: BCTF{q0000000000b3333333333-ju57-w0n-pwn20wn!!}題目描述：It seems easy, right?Tip: openssl rsautl -encrypt -in FLAG -inkey public.pem -pubin -out flag.enc
題目給了一個flag.enc，還有一個public.pem，附件下載地址：

https://adworld.xctf.org.cn/media/task/attachments/9244cc370caa43f491636f8c4670fe7d.zip

安裝openssl可以讀取到n和e，因為n不大，可以在yafu或者factordb.com上分解得到n=p * q * r
根據flag.enc，可以得到密文m
根據中國剩餘定理，我們要求得m在p，q，r下的餘數，不妨設為pmod，qmod，rmod
然後根據模三次剩餘，即：proot ^ 3 ≡ pmod ( mod p），求得：proot，同理求得qroot，rroot
利用網頁工具可以直接計算得到：

x^3 = 19342563376936634263836075415482 (mod 27038194053540661979045656526063) - Wolfram|Alpha

Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels.

www.wolframalpha.com

我們從openssl命令行得到一個似乎是通過RSA加密的密文。我們還可以訪問公鑰，因此我們像使用標準RSA密碼一樣，通過恢復參數來執行以下操作：
e=3
n=23292710978670380403641273270002884747060006568046290011918413375473934024039715180540887338067
使用YAFU，我們將模量分為：
p=26440615366395242196516853423447
q=27038194053540661979045656526063
r=32581479300404876772405716877547
我們得到三個質數。這仍然是好的，這可能只是多質RSA。這一點也不奇怪，總的來說很簡單(p-1)(q-1)(r-1)，其餘的計算照常進行。但它不存在，因為我們發現模乘逆不存在。原因很明顯：gcd(e，to客戶端)=3，應該是1。這不是我們第一次遇到類似的情況（如https://github.com/p4-team/ctf/tree/master/2015-10-18-hitcon/crypto 314-u rsabin-35；eng版本），所以我們對如何處理這個問題有了一些想法。
在應用RSA解碼之前，我們需要去掉這3個。這意味著加密是：
ciphertext=plaintext^e mod n=(plaintext^e')^3 mod n
所以如果我們能形成方程兩邊的模三次根(mod n)，我們就可以用e'=e/3進行RSA譯碼。因為e=3，所以e'=e/3=1，所以這裡並不容易，這意味著我們的加密是簡單的：
ciphertext=plaintext^3 mod n
所以整個解密過程需要密文中的模立方根(mod n)。
一些關於模根的閱讀使我們得出結論，這是可能的，但只有在有限的領域。所以它不能對n做，這是一個複合數，我們知道它是，因為它是pqr。
這個問題讓我們想起了中文提醒定理（ https://en.wikipedia.org/wiki/Chinese_remainder_theorem ），我們考慮了一會兒，我們想到了一個想法，如果我們能從密文（mod prime）中計算出3個素數的三次模根，我們就能計算出合併根。我們可以用高斯算法（http://www.di-mgt.com.au/crt.html#gaussalg）來實現這一點。
所以我們繼續計算：
pt^3 mod p=ciperhtext mod p=20827907988103030784078915883129
pt^3 mod q=ciperhtext mod q=19342563376936634263836075415482
pt^3 mod r=ciperhtext mod r=10525283947807760227880406671000
然後我們花了一段時間來解決pt的這個方程，最後我們發現wolframalpha實現了這個功能，例如：

x^3 = 2 - Wolfram|Alpha

Wolfram|Alpha brings expert-level knowledge and capabilities to the broadest possible range of people—spanning all professions and education levels.

www.wolframalpha.com